Production-Ready AAD with Smoothing: 90% reduction in computational cost for autocallable Greeks using Automatic Adjoint Differentiation and mathematical smoothing
WBS Quantitative Finance Conference, Palermo • September 2025
View Presentation Slides →At the 21st annual WBS Quantitative Finance Conference in Palermo (September 2025), several presentations focused on computing autocallable Greeks, highlighting the active research in this space. MatLogica contributed a practical, production-ready implementation with concrete cost savings, including a complete open-source methodology.
Conference discussions validated the urgent need for robust solutions for the significantly sized ($104B) autocallable market, with participants ranging from major banks, specialized boutiques, and hedge funds, all wrestling with the same Greeks calculation challenges.
Despite AAD adoption by ~20% of Tier 1 banks, the debate over computing autocallable Greeks remains unsettled. A vocal contingent argues that "AAD doesn't work for discontinuous payoffs," while others persist with expensive bump-and-revalue approaches.
Bump-and-revalue leaves you stuck with 10M+ paths for stable correlation Greeks, noisy results OTM, and uncertain bump sizes introducing error rates of up to 10%. Moreover, this is for a $104B annual market comprising 66% of structured products issuance!
Pathwise AAD requires continuous payoffs, and standard application to digitals yields zero gradients almost everywhere. However, dismissing AAD entirely would mean losing the methodology's significant efficiency gains.
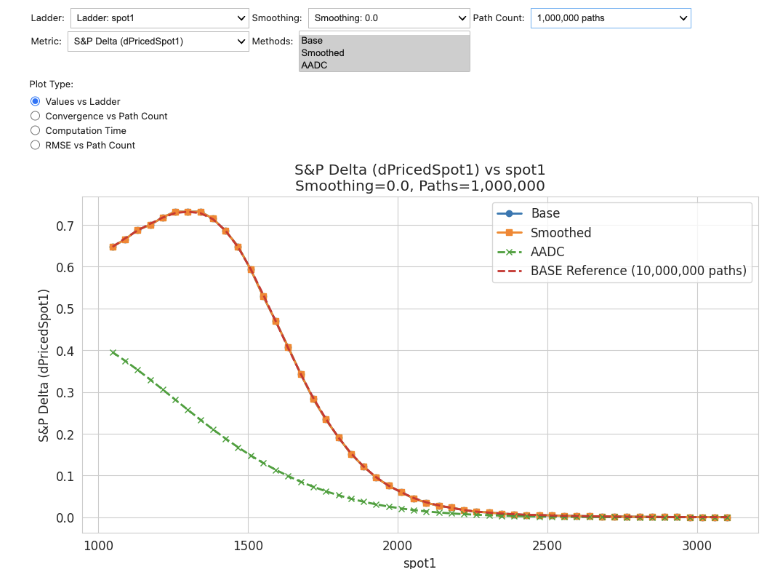
AAD without smoothing produces incorrect results for discontinuous payoffs
The key insight is that you don't need to work with the discontinuous payoff directly. Replace Heaviside functions with smooth sigmoid approximations that preserve contract economics.
contLess(a, b, h) =
h = 0: 1{a < b}
h > 0: ½(((b-a)/(0.02h))/√(1+((b-a)/(0.02h))²) + 1)
Three methods benchmarked on Phoenix Autocallable:
Phoenix Autocallable test case:
Smoothed payoffs with AAD deliver the best accuracy-per-cost ratio. The correlation Greeks that required 10M paths with bump-and-revalue become tractable at 1M.
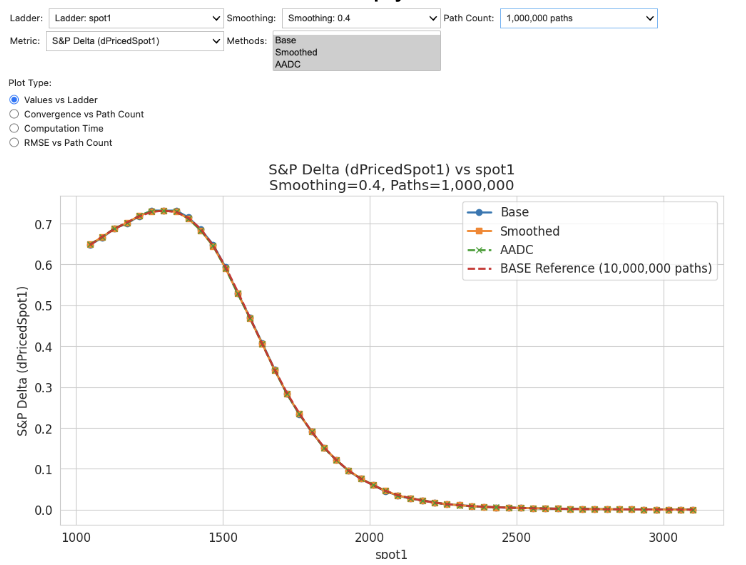
Delta ladder showing stable Greeks across spot levels with AADC method
The area difference between smoothed and actual digital is quantifiable. Convolute with density for measurable price deviation. In practice, relative error is small for material payoffs and negligible when digital value itself is small (i.e., when it doesn't matter).
Gamma via bump-and-revalue of AAD delta (far more stable than double-bumping price). Smoothing ensures finite differences remain well-behaved for higher orders.
Rotation of coordinates technique (Rakhmonov & Rakhmonov, 2019) for smooth worst-of sampling. Demonstrated for 2 assets, the principle scales naturally to N underlyings.
Everything available for validation:
Try it yourself: Clone repo, run benchmarks, validate against your implementations. Contribute: Pull requests welcome for extensions, new test cases, or methodology improvements.